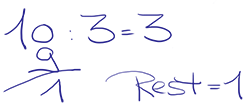IBAN in Excel per Formel berechnen

Im August 2014 ist die IBAN verpflichtend eingeführt worden – die International Bank Account Number, kurz IBAN. Hinter der IBAN verbirgt sich keine komplizierte Mathematik. Allerdings stoßen wir bei der Berechnung der Prüfziffer an die Grenzen von Excel. Warum? Excel rechnet mit einer Genauigkeit von 15 Stellen. Die Zahl, die zur Ermittlung der Prüfziffer herangezogen wird hat 24 Stellen. Die Problemlösung findest du hier!
Passende Schulungen
Excel Grundlagen
Excel Grundlagen: Der Excel Grundkurs für deinen Einstieg in MS Excel

Excel Aufbau
Excel Aufbau Seminar: Fortgeschrittene Excel Funktionen optimal nutzen

Aufbau der IBAN
Die Einführung der IBAN bedeutet nicht, dass du dich von deiner Kontonummer und Bankleitzahl verabschieden musst, du musst das Ganze nur anders schreiben und um zwei Informationen ergänzen.
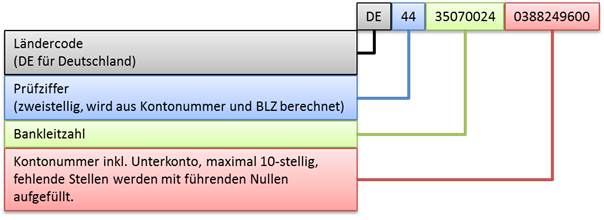
Betrachten wir einen inländischen Bankkunden mit der Bankleitzahl 35070024 und der Kontonummer 3882496. Die IBAN des Kunden sieht nach der Umstellung so aus:
Neben dem vorangestellten Ländercode sind drei weitere Dinge zu berücksichtigen.
- Die Kontonummer muss mit der Unterkontonummer (meist 00) angegeben werden.
- Ist die Kontonummer inkl. Unterkontonummer kürzer als 10 Stellen, wird diese mit führenden Nullen auf 10 Stellen aufgefüllt.
- Die Prüfziffer muss berechnet werden.
Mit welcher Formel wird die Prüfziffer berechnet?
Die Antwort lautet ganz offiziell: Die Berechnung der Prüfziffer erfolgt gemäß ISO 7064 per Modulo 97-10.
Das hört sich komplizierter an, als es ist. Allerdings sind hier einige Schrittfolgen nötig, die ich an dieser Stelle an unserem Beispiel erklären möchte.
Passende Schulungen
Excel Kompakt
Der Excel Kurs: Werde zum Profi in fünf Tagen - auch online

Zuerst wird aus Kontonummer und Bankleitzahl die BBAN (Basic Bank Account Number) kreiert. Also wird aus Bankleitzahl 35070024 und der Kontonummer 0388249600 die BBAN 350700240388249600.
Anschließend werden die beiden Zeichen der Länderkennung sowie weitere eventuell in der Kontonummer enthaltene Buchstaben in rein numerische Ausdrücke umgewandelt. Die Grundlage für die Zahlen, die aus den Buchstaben gebildet werden sollen, bildet ihre Position der jeweiligen Zeichen im lateinischen Alphabet. Zu diesem Zahlenwert wird 9 addiert. Die Summe ergibt die Zahl, die den jeweiligen Buchstaben ersetzen soll. Dementsprechend steht für A (Position 1+9) die Zahl 10, für D (Position 4+9) die 13 und für E (Position 5+9) die 14. Der Länderkennung DE entspricht also die Ziffernfolge 1314.
Im nächsten Schritt wird diese Ziffernfolge an die BBAN angehängt und es werden noch 2 Nullen angefügt. Hieraus ergibt sich 350700240388249600131400.
Hier noch einmal die bisherigen Schritte zusammengefasst:
| 10 stellige Kontonummer (inkl. Unterkontonummer) | 0388249600 |
| Bankleitzahl | 35070024 |
| Zusammenfügen der Nummern zur BBAN | 350700240388249600 |
| Ermittlung der Zahlenwerte für die Länderkennung | D = 4 + 9 = 13 E= 5 + 9 = 14 |
| Anfügen der Zahlenwerte für D und E | 3507002403882496001314 |
| Hinzufügen von 2 Nullen an das Ende der Zahlenkolonne | 350700240388249600131400 |
Aus dieser, bei deutschen Konten immer 24-stellige Zahl, wird nun die Prüfziffer nach dem folgenden Verfahren berechnet:
Die 24-stelligen Zahl wird durch 97 geteilt und der Rest wird ermittelt.
Anmerkung:
In Zeiten der digitalen Verarbeitung von Zahlen kennt man ja fast nur noch Dezimalzahlen. Das Teilen mit Rest haben wir mal in der Schule gelernt. Vielleicht erinnern Sie sich noch: 10 geteilt durch 3 ist 3 Rest 1.
In Excel lässt sich dieser Rest mit der Funktion REST() normalerweise problemlos ermitteln.
Das Ergebnis ist für dieses Beispiel 54. Dieses Ergebnis wird von der nach ISO-Standard festgelegten Zahl 98 subtrahiert. Es ergibt sich die Prüfziffer 44. Ist das Resultat kleiner als Zehn, so wird der Zahl eine Null vorangestellt, sodass sich wieder ein zweistelliger Wert ergibt. Aus der Länderkennung, der zweistelligen Prüfziffer und der BBAN wird nun die IBAN generiert. Die ermittelte IBAN lautet in unserem Beispiel: DE44350700240388249600.
So „trickst“ man Excel aus
Gar nicht so schwer, wenn uns da nicht die 15-stellige Genauigkeit von Excel einen Strich durch die Rechnung machen würde. Leider ist Excel nicht in der Lage mit mehr als 15 Stellen zu rechnen – wenn man einmal von wilden mathematischen Konstrukten und der VBA Programmierung absieht. Excel scheitert also schon bei der Darstellung der 24-stelligen Zahl. Hier könnten wir noch mit entsprechenden Formatierungen reagieren, aber bei der einfachen Ermittlung des Restwertes steigt Excel vollends aus und quittiert unsere Mühen entweder mit einer Fehlermeldung oder die 24-stellige Zahl wird ab der 15ten Stelle nur mit Nullen aufgefüllt.
Diese Hürde könnte man umgehen, indem man VBA Code nutzt, aber es geht auch einfacher.
Für die Berechnung der IBAN kursiert im Internet folgende Formel:
=“DE“&TEXT((98-REST((62*(1+REST(A2;97))+27*REST(B2;97));97));“00″)&A2&TEXT(B2;“0000000000″)
Wer es vorzieht das Ergebnis in besser lesbaren Vierergruppen darzustellen verwendet diese Formel:
=“DE“&TEXT((98-REST((62*(1+REST(A2;97))+27*REST(B2;97));97));“00″)&(TEXT(A2;“ 0000 0000 „)&TEXT(B2;“0000 0000 00“))
Anmerkung:
Da diese Formel auf den unterschiedlichsten Seiten im Netz auftaucht, ist die ursprüngliche Quelle nicht eindeutig bestimmbar. Ich danke dem ursprünglichen Verfasser für seine Arbeit und würde mich freuen zu erfahren, wer auf diese Idee gekommen ist und vor allem wie die Lösung mathematisch zustande kam. Sollte jemand den Urheber kennen oder sich berufen fühlen die Entstehung der Formel zu erklären, so kann gerne ein Kommentar hinterlassen werden.
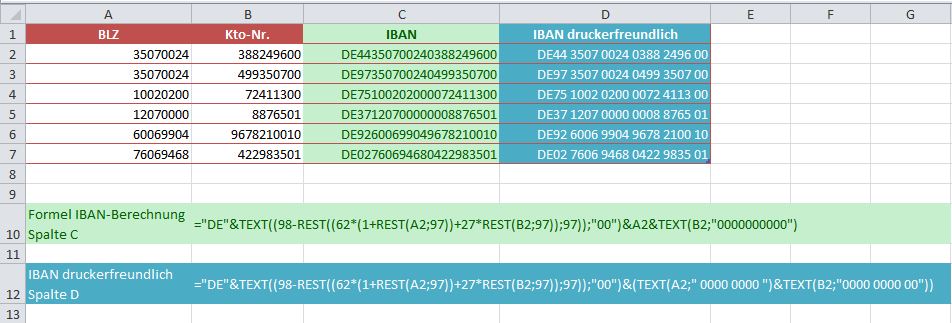
Hier sehen wir das Ergebnis in einer Exceltabelle:
Wer dem Braten nicht traut, kann seine Ergebnisse auf diversen Internetseiten mit IBAN-Umrechnern kontrollieren.
Z.B. hier IBAN Rechner
Sei nicht irritiert, wenn ein IBAN Rechner etwas an den o.g. Daten bemängelt. Die Kontonummern sind der Phantasie des Autoren entsprungen. Probiere es einfach mit deinen Bankdaten aus.
Kontakt

„*“ zeigt erforderliche Felder an